Generating All Subsets of a Set

A subset is an unordered selection of elements from a set. The size of a subset may be equal to or less than the size of its superset.

To build a subset, we can make two choices for each element in the set: either include it in the subset or don’t. Since the order of the elements in the subset does not matter, the number of possible subsets for a set of length $n$ is given by:

$$\underbrace{2 \times 2 \times 2 \times \dots \times 2}_{n \text{ times}} = 2^n$$

Method 1: Recursion With Backtracking

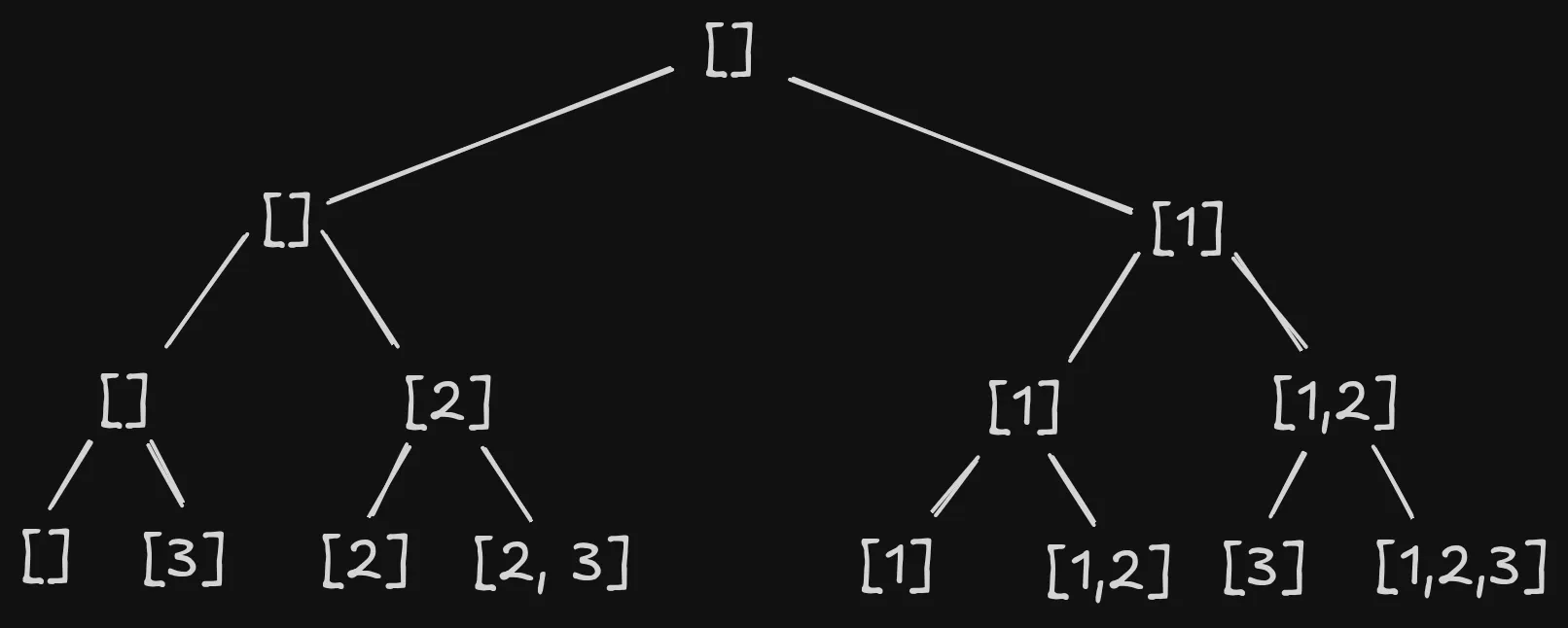
For this method, we keep track of the current subset being built and the depth of recursion. When $\text{depth} = n$, we have a complete subset which we can then process.

At each iteration, we do 2 recursive calls - one that includes the current element being considered into the subset and one that doesn’t. When we have finished building the subset, we can then backtrack to process the other subsets.

void processSubset(const std::vector<int>& subset) {
    // ...
}

std::vector<int> subset;

void backtrack(const std::vector<int>& set, int depth) {
    if (depth == set.size()) {
        processSubset(subset);
        return;
    }

    backtrack(set, depth + 1);

    subset.push_back(set[depth]);
    backtrack(set, depth + 1);
    subset.pop_back();
}

void generateSubsets(const std::vector<int>& set) {
    backtrack(set, 0);
}

Time complexity: $O(n \times 2^n)$, there are $2^n$ subsets and each subset takes $n$ iterations to process. If we did not process the subsets however, the time complexity would be $O(2^n)$
Space complexity: $O(n)$, the maximum depth of recursion is $n$ and we need to store at most $n$ elements in a temporary subset.

Method 2: Bit Manipulation

As stated previously, we have to make two choices per element in the set to build a subset. These choices can be represented by a sequence of bits. When a bit is 1, the element it represents is included in the subset.

Let’s see what this means for an example set $S = \{1, 2\}$

Decimal	Bits	Subset
0	00	[]
1	01	[1]
2	10	[2]
3	11	[1, 2]

You can see that each subset is represented by a unique combination of bits.

To implement this method in code, we need to iterate over all numbers $0 \dots (2^n - 1)$. At each iteration, we check which bits are 1 and add the corresponding elements to the subset.

void processSubset(const std::vector<int>& subset) {
    // ...
}

void generateSubsets(const std::vector<int>& set) {
    // 2 ^ set.size();
    const int numSubsets = 1 << set.size();

    std::vector<int> subset;
    for (int subsetIndex = 0; subsetIndex < numSubsets; subsetIndex++) {
        for (int i = 0; i < set.size(); i++) {
            if (subsetIndex & (1 << i)) {
                subset.push_back(set[i]);
            }
        }

        processSubset(subset);
        subset.clear();
    }
}

Time complexity: $O(n \times 2^n)$, there are $2^n$ subsets and each subset takes $n$ iterations to build.
Space complexity: $O(n)$, we need to store at most $n$ elements in a temporary subset.